前回の続き。
以下 、n*n魔方陣をn次魔方陣と呼ぶことにする。
さて、ここで5次魔方陣を作りたいと思う。 これも4次魔方陣と同様に半魔方陣を２つ見つけてくればいい。 次の二つが見つかる。
この二つを組み合わせたものに a , b , c , d に 1 , 2 , 3 , 4
そして A , B , C , D に0 , 5 , 10 , 15 , 20 を適当に代入してやると、 魔方陣が完成する。
さてここで7次魔方陣などを作るとき半魔方陣を見つけるのは 大変である。そこで上の5次半魔方陣をよく見ると次のことに気づく。
・左の場合、上の段を 2つ右にずらしたものがそのすぐ下の段になっている
・右の場合、上の段を 3つ右にずらしたものがそのすぐ下の段になっている
これは一般 にn次魔方陣において、n が2と3の倍数でないときに同様のことが言える。
さらに一般化したものを数学的に書けばこうである。
まず、半魔方陣の i 行 j 列の数を（ i , j )で表すものとする。
定理１ a , b を正の整数とし、n が a , a - 1 , a + 1 , b , b - 1 , b + 1 とそれぞれ互いに素とする。このとき （ i , k + a * i mod n）、（i = 1,2, ... ,n） に （ １ , k ） と同じ記号をいれるとそれは半魔方陣となる。また、（ i , k + b * i mod n）に (1 , k ) と同じ記号をいれるとそれも半魔方陣となる。 [証明] （また別の機会にする）//
さらに b - a と nが互いに素となるようにとれば二つの半魔方陣は重ならない。
n が奇数で 3 の倍数でないときは a = 2 で考えればよい。
たとえばn = 7の場合を考える上の定理で a = 2 , b = 3を考えると次の二つの半魔方陣が得られる。
コレを用いて、a = 0 , b = 1 , c = 2 , d = 3 , e = 4 , f = 5 , g = 6 ,
A = 0 , B = 7 , C = 14 , D = 21 , E = 28 , F = 35 , G = 42
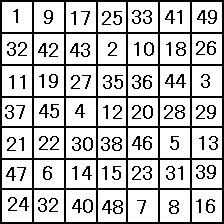
として魔方陣を構成すると下のようになる。
p を 5 以上の素数として、p次魔方陣をつくるときは 定理において a = 2, b = 3で計算すればよい。
(なぜならば、a - 1 = 1 , a + 1 = 3 , b - 1 = 2 , b + 1 = 2^2であるから素数 p とは互いに素となる)
そしてm次魔方陣とn次魔方陣が与えられたとき、m魔方陣のマスにn次魔方陣を挿入してm魔方陣の数字にm^2を掛けたものを挿入したn次魔方陣に加えることで、m*n次魔方陣を作ることが出来る。
つまりm次魔方陣の i 行 j 列の数を A( i , j ) , n次魔方陣の i 行 j 列の数を B(i , j)としてあらわし、これから作るm*n次魔方陣の i 行 j列の数を X(i , j)とし
bをsで割った商を Q1 , 余りを r1 , bをtで割った商を Q2 , 余りを r2とすると
X( i , j ) = A(Q1 , Q2) * b^2 + B (r1 , r2)
となるように X( i , j ) の値を定めていくとm*n次魔方陣を構成できる。
3次魔方陣は簡単に求められるので、そのことと今までの話から、n = 2 (mod 4) となる場合を除けばすべての次元で魔方陣 を構成できる。
PR
